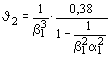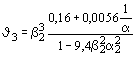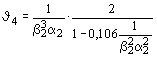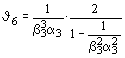РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
И СОЕДИНЕНИЙ
4.6*. Расчетные сопротивления проката для различных видов напряженных состояний следует определять по формулам, приведенным в табл. 48*.
Таблица 48*
|
Напряженное состояние |
Расчетные сопротивления проката |
|
Растяжение, сжатие и изгиб: |
|
|
по пределу текучести |
Ry = Ryn / gm |
|
по временному сопротивлению |
Ru = Run / gm |
|
Сдвиг |
Rs = 0,58 Ryn / gm |
|
Смятие торцевой поверхности
(при наличии пригонки) |
Rp = Run / gm |
|
Смятие местное в цилиндрических шарнирах (цапфах) при плотном касании |
Rtp = 0,5 Run / gm |
|
Диаметральное сжатие катков
(при свободном касании
в конструкциях с ограниченной подвижностью) |
при Run Ј 600 МПа (5886 кгс/см2) Rcd = 0,25 Run / gm ;
при Run > 600 МПа (5886 кгс/см2) Rcd = [0,042Ч10-6 (Run - 600)2 +
+ 0,025] Run / gm, МПа ;
Rcd = [0,0438Ч10-8 (Run - 5886)2 +
+ 0,025] Run / gm, кгс/см2 |
|
Растяжение в направлении толщины проката t при t до 60 мм |
Rth = 0,5 Run / gm |
П р и м е ч а н и е. gm - коэффициент надежности по материалу, определяемый в соответствии с п. 4.7*.
4.7*. Значения коэффициента надежности gm по материалу проката следует принимать по табл. 49*.
Таблица 49*
|
Государственный стандарт
(марка стали или значение предела текучести) |
Коэффициент
надежности
по материалу gm |
|
ГОСТ 535-88 и
ГОСТ 14637-89 [Ст3сп, Ст3пс, Ст3кп]
ГОСТ 19281-89 и
ГОСТ 19282-89 [до 380 МПа (39 кгс/мм2)] |
1,05 |
|
ГОСТ 19281-89 и
ГОСТ 19282-89
[св. 380 МПа (39 кгс/мм2)] |
1,10 |
|
ГОСТ 6713-91 [16Д] |
1,09 |
|
ГОСТ 6713-91 [15ХСНД] |
1,165 |
|
ГОСТ 6713-91 [10ХСНД] |
1,125 |
Нормативные и расчетные сопротивления проката из сталей по ГОСТ 6713-91, сталей марок 390-14Г2АФД, 390-15Г2АФДпс по ГОСТ 19281-89 и стали марки 40Х13 по ГОСТ 5632-72 следует принимать по табл. 50*.
Таблица 50*
|
Марка стали |
Государст- |
Прокат |
Толщина |
Нормативное сопротивление2, МПа (кгс/мм2) |
Расчетное сопротивление3, МПа (кгс/см2) |
|
|
венный стандарт |
|
проката1,
мм |
по пределу текучести Ryn |
по временному сопротивлению Run |
по пределу текучести Ry |
по временному сопротивлению Ru |
|
16Д |
ГОСТ 6713-91 |
Любой |
До 20 |
235 (24) |
370 (38) |
215 (2200) |
340 (3450) |
|
16Д |
ГОСТ 6713-91 |
« |
21-40 |
225 (23) |
370 (38) |
205 (2100) |
340 (3450) |
|
16Д |
ГОСТ 6713-91 |
« |
41-60 |
215 (22) |
370 (38) |
195 (2000) |
340 (3450) |
|
15ХСНД |
ГОСТ 6713-91 |
« |
8-32 |
340 (35) |
490 (50) |
295 (3000) |
415 (4250) |
|
15ХСНД |
ГОСТ 6713-91 |
Листовой |
33-50 |
330 (34) |
470 (48) |
285 (2900) |
400 (4100) |
|
10ХСНД |
ГОСТ 6713-91 |
Любой |
8-15 |
390 (40) |
530 (54) |
350 (3550) |
470 (4800) |
|
10ХСНД |
ГОСТ 6713-91 |
Листовой |
16-32 |
390 (40) |
530 (54) |
350 (3550) |
470 (4800) |
|
10ХСНД |
ГОСТ 6713-91 |
« |
33-40 |
390 (40) |
510 (52) |
350 (3550) |
450 (4600) |
|
390-15Г2
АФДпс |
ГОСТ 19282-89 |
« |
4-32 |
390 (40) |
540 (55) |
355 (3600) |
490 (5000) |
|
390-14
Г2АФД |
ГОСТ 19282-89 |
« |
4-50 |
390 (40) |
540 (55) |
355 (3600) |
490 (5000) |
|
40Х13 |
ГОСТ 5632-72 |
Круглый |
До 250 |
1200 (122) |
1540 (157) |
1050 (10700) |
1365 (13900) |
1 За толщину фасонного проката следует принимать толщину полки.
2 За нормативные сопротивления приняты минимальные значения предела текучести и временного сопротивления, приведенные в ГОСТ 6713-91 в кгс/мм2. Нормативные сопротивления в МПа вычислены умножением соответствующих величин на множитель 9,80665 и округлением до 5 МПа.
3 Здесь указаны расчетные сопротивления растяжению, сжатию и изгибу Ry и Ru. Остальные расчетные сопротивления определяются по формулам табл. 48*.
Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициент надежности по материалу, определяемым по табл. 49*, и округлением до 5 МПа.
Расчетные сопротивления проката по ГОСТ 535-88, ГОСТ 14637-89 и ГОСТ 19281-89 следует принимать равными пределу текучести, указанному в этих стандартах, поделенному на коэффициент надежности по материалу gm по табл. 49*.
4.8. Расчетные сопротивления отливок из углеродистой и легированной сталей следует принимать по табл. 51*.
Таблица 51*
|
|
Расчетные сопротивления, МПа (кгс/см2), отливок |
|
Напряженное |
обо- |
из стали марки |
|
состояние |
значение |
25Л |
30Л |
35Л |
20ГЛ |
20ФЛ |
35ХН2МЛ |
35ГЛ |
|
Растяжение, сжатие и изгиб |
Ry |
175 (1800) |
190 (1950) |
205 (2100) |
205 (2100) |
220 (2250) |
400 (4100) |
220 (2250) |
|
Сдвиг |
Rs |
105 (1100) |
115 (1200) |
125 (1300) |
125 (1300) |
130 (1350) |
240 (2450) |
130 (1350) |
|
Смятие торцевой поверхности (при наличии пригонки) |
Rp |
265 (2700) |
300 (3050) |
315 (3200) |
345 (3500) |
315 (3200) |
440 (4500) |
345 (3500) |
|
Смятие местное в цилиндрических шарнирах (цапфах) при плотном касании |
Rtp |
125 (1300) |
145 (1500) |
155 (1600) |
170 (1750) |
155 (1600) |
222 (2250) |
170 (1750) |
|
Диаметральное сжатие катков (при свободном касании в конструкциях с ограниченной подвижностью) |
Rcd |
7
(70) |
7,5 (75) |
8
(80) |
9
(90) |
8
(80) |
11 (110) |
9
(90) |
4.9. Расчетные сопротивления поковок из углеродистой и легированной сталей следует принимать по табл. 52*.
Таблица 52*
|
Напряженное |
Расчетное сопротивление, МПа (кгс/см2),
поковок группы IV |
|
|
состояние |
обо- |
при категории прочности (марке стали) |
|
|
|
значение |
КП275
(Ст5сп2) |
КП245
(20-а-Т) |
КП315
(35-а-Т) |
КП345
(45-а-Т) |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Растяжение, сжатие и изгиб |
Ry |
215 (2200) |
205 )2100) |
260 (2650) |
290(2950) |
|
|
Сдвиг |
Rs |
120 (1250) |
115 (1200) |
145 (1500) |
165 (1700) |
|
|
Смятие торцевой поверхности (при наличии пригонки) |
Rp |
325 (3300) |
310 (3150) |
395 (4000) |
435 (4400) |
|
|
Смятие местное в цилиндрических шарнирах (цапфах) при плотном касании |
Rtp |
160 (1650) |
150 (1550) |
195 (2000) |
215 (2200) |
|
|
Диаметральное сжатие катков (при свободном касании в конструкциях с ограниченной подвижностью) |
Rcd |
8 (80) |
7,5 (75) |
11 (110) |
10 (100) |
|
Окончание табл. 52*
|
Напряженное |
Расчетное сопротивление, МПа (кгс/см2),
поковок группы IV |
|
|
состояние |
обо- |
при категории прочности (марке стали) |
|
|
|
значение |
КП315
(30Г-2-Т) |
КП345
(35Г-2-Т) |
КП785
(40ХН2МА-2-2-Т) |
КП1200
(40Х13) |
|
|
1 |
2 |
7 |
8 |
9 |
10 |
|
Растяжение, сжатие и изгиб |
Ry |
260 (2650) |
280 (2850) |
605 (6150) |
1050 (10700) |
|
|
Сдвиг |
Rs |
145 (1500) |
160 (1650) |
350 (3550) |
610 (6200) |
|
|
Смятие торцевой поверхности (при наличии пригонки) |
Rp |
395 (4000) |
420 (4250) |
905 (9200) |
1365 (13900) |
|
|
Смятие местное в цилиндрических шарнирах (цапфах) при плотном касании |
Rtp |
195 (2000) |
205 (2100) |
450 (4600) |
685 (6950) |
|
|
Диаметральное сжатие катков (при свободном касании в конструкциях с ограниченной подвижностью) |
Rcd |
10 (100) |
10 (100) |
23 (230) |
85 (860) |
|
4.10. Расчетные сопротивления сварных соединений для различных видов соединений и напряженных состояний следует определять по формулам, приведенным в табл. 53.
Таблица 53
|
Сварные соединения |
Напряженное состояние |
Расчетные сопротивления сварных соединений |
|
Стыковые |
Сжатие.
Растяжение и изгиб при автоматической, полуавтоматической или ручной сварке с физическим контролем качества швов: |
|
|
|
по пределу текучести |
Rwy = Ry |
|
|
по временному сопротивлению |
Rwu = Ru |
|
|
Сдвиг |
Rws = Rs |
|
С угловыми |
Срез (условный): |
|
|
швами |
по металлу шва |
Rwf = 0,55 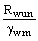 |
|
|
по металлу границы сплавления |
Rwz = 0,45 Run |
П р и м е ч а н и я: 1. Для швов. выполняемых ручной сваркой, значения Rwun следует принимать равными значениям временного сопротивления разрыву металла шва. указанным в ГОСТ 9467-75*.
2. Для швов, выполняемых автоматической или полуавтоматической сваркой, значения Rwun следует принимать по разд. 3 СНиП II-23-81*.
3. Значение коэффициента надежности по материалу шва gwm следует принимать равным 1,25.
Расчетные сопротивления стыковых соединений элементов из сталей с разными расчетными сопротивлениями следует принимать как для стыковых соединений из стали с меньшим значением расчетного сопротивления.
Расчетные сопротивления металла швов сварных соединений с угловыми швами следует принимать по прил. 2. СНиП II-23-81*.
4.11*. Расчетные сопротивления одноболтовых соединений следует определять по формулам, приведенным в табл. 54*.
Таблица 54*
|
|
Расчетные сопротивления одноболтовых соединений |
|
Напряженное состояние |
срезу и растяжению болтов
при классе прочности
или марке стали |
смятию
соединяемых |
|
|
4.6; Ст3сп4; 09Г2;
295-09Г2-4; 295-09Г226; 325-09Г2С-4; 325-09Г2С-6 |
40Х |
элементов из стали
с нормативным
пределом текучести до 440 МПа (4500 кгс/см2) |
|
Срез |
Rbs = 0,38 Rbun |
Rbs = 0,4 Rbun |
- |
|
Растяжение |
Rbt = 0,42 Rbun |
Rbt = 0,5 Rbun |
- |
|
Смятие: |
|
|
|
|
а) болты класса точности А |
- |
- |
Rbp = 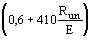 Run Run |
|
б) болты классов точности В и С |
- |
- |
Rbp = 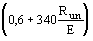 Run Run |
Расчетные сопротивления срезу и растяжению болтов следует принимать по табл. 55*.
Таблица 55*
|
Напряженное |
Расчетное сопротивление, МПа (кгс/см2), болтов
при классе прочности или марке стали |
|
состояние |
обозначение |
4.6 |
Ст3сп4 |
09Г2;
295-09Г24;
295-09Г2-6 |
325-09Г2С-4; 325-09Г2С-6 |
40Х |
|
Срез |
Rbs |
145 (1500) |
140 (1450) |
154 (1700) |
175 (1800) |
395 (4000) |
|
Растяжение |
Rbt |
160 (1650) |
155 (1600) |
185 (1900) |
195 (2000) |
495 (5000) |
Расчетные сопротивления смятию элементов, соединяемых болтами, следует определять по прил. 2 СНиП II-23-81*.
4.12*. Расчетное сопротивление растяжению фундаментных (анкерных) болтов Rba следует определять по формуле
Rba = 0,4 Run . (138)
Расчетные сопротивления растяжению фундаментных (анкерных) болтов следует принимать по табл. 56*.
Таблица 56*
|
Диаметр болтов d, |
Расчетные сопротивления, МПа (кгс/см2),
фундаментных (анкерных) болтов из стали марок |
|
мм |
20 |
09Г2;
295-09Г2-6 |
325-09Г2С-6 |
40Х |
|
12-20 |
160 (1650) |
175 (1800) |
185 (1900) |
- |
|
16-27 |
- |
- |
- |
430 (4400) |
|
21-32 |
160 (1650) |
175 (1800) |
180 (1850) |
- |
|
30 |
- |
- |
- |
370 (3800) |
|
36 |
- |
- |
- |
295 (3000) |
|
33-60 |
160 (1650) |
- |
180 (1850) |
- |
|
42 |
- |
- |
- |
255 (2600) |
|
48 |
- |
- |
- |
235 (2400) |
|
61-80 |
160 (1650) |
- |
175 (1800) |
- |
|
81-100 |
160 (1650) |
- |
170 (1750) |
- |
|
101-160 |
160 (1650) |
- |
170 (1750) |
- |
|
161-250 |
160 (1650) |
- |
- |
- |
|
4.13. Расчетное сопротивление срезу для сплава ЦАМ 9-1,5Л следует принимать равным 50 МПа (500 кгс/см2).
4.14. Расчетное сопротивление высокопрочных болтов по ГОСТ 22353-77* и ГОСТ 22356-77* растяжению Rbh следует определять по формуле
Rbh = 0,7 Rbun , (139)
где Rbun - наименьшее временное сопротивление высокопрочных болтов разрыву по ГОСТ 22356-77*.
4.15*. Значения коэффициента трения m по соприкасающимся поверхностям деталей во фрикционных соединениях1 следует принимать по табл. 57*. Способ обработки контактных поверхностей должен быть указан в чертежах КМ.
1 Фрикционными называются соединения, в которых передача усилия осуществляется только силами трения по контактным плоскостям соединяемых элементов, возникающего вследствие натяжения высокопрочных болтов.
Таблица 57*
|
Способ обработки контактных поверхностей
во фрикционных соединениях |
Коэффициент трения m |
|
1. Пескоструйный или дробеструйный двух поверхностей кварцевым песком или дробью - без последующей консервации |
0,58 |
|
2. Кварцевым песком или дробью одной поверхности с консервацией полимерным клеем и посыпкой карборундовым порошком, стальными щетками без консервации - другой поверхности |
0,50 |
|
3. Газопламенный двух поверхностей без консервации |
0,42 |
|
4. Стальными щетками двух поверхностей без консервации |
0,35 |
|
5. Дробеметный двух поверхностей дробью без последующей консервации |
0,38 |
|
6. Дробеметный двух поверхностей дробью с последующим их газопламенным нагревом (до температуры 250-300 °С) на кольцевых зонах вблизи отверстий площадью не менее площади шайбы |
0,61 |
4.16. Расчетное сопротивление растяжению Rdh высокопрочной стальной проволоки, применяемой в пучках и канатах из параллельно уложенных проволок, следует определять по формуле
Rdh = 0,63 Run , (140)
где Run - наименьшее временное сопротивление проволоки разрыву по государственным стандартам или техническим условиям.
4.17*. При определении расчетного сопротивления стального витого каната с металлическим сердечником учитываются значение разрывного усилия каната в целом, установленное государственным стандартом или техническими условиями на канаты (а при его отсутствии в нормах - значение агрегатной прочности витого каната) и коэффициент надежности gm = 1,6.
4.18*. Модуль упругости или модуль сдвига прокатной стали, стального литья, пучков и канатов из параллельно уложенных проволок следует принимать по табл. 58*.
Таблица 58*
|
Полуфабрикаты |
Модуль упругости Е или модуль сдвига G, МПа (кгс/см2) |
|
1. Прокатная сталь и стальное
литье |
Е = 2,06 Ч 105 (2,1 Ч 106) |
|
2. То же |
G = 0,78 Ч 105 (0,81 Ч 106) |
|
3. Пучки и канаты из параллельно уложенных оцинкованных проволок по ГОСТ 3617-71 |
Е = 2,01 Ч 106 (2,5 Ч 106) |
Модуль упругости стальных оцинкованных витых канатов с металлическим сердечником, подвергнутых предварительной вытяжке усилием, равным половине разрывного усилия каната в целом, следует принимать по табл. 59.
Таблица 59
|
Канаты |
Кратность свивки |
Модуль упругости Е, МПа (кгс/см2) |
|
|
6 |
1,18 Ч 105 (1,20 Ч 106) |
|
Одинарной свивки |
8 |
1,45 Ч 105 (1,47 Ч 106) |
|
по ГОСТ 3064-80 |
10 |
1,61 Ч 105 (1,63 Ч 106) |
|
и закрытые несущие |
11 |
1,65 Ч 105 (1,67 Ч 106) |
|
по ТУ 14-4-1216-82 |
12 |
1,70 Ч 105 (1,73 Ч 106) |
|
|
14 |
1,75 Ч 105 (1,78 Ч 106) |
|
|
16 |
1,77 Ч 105 (1,80 Ч 106) |
УЧЕТ УСЛОВИЙ РАБОТЫ И НАЗНАЧЕНИЯ КОНСТРУКЦИЙ
4.19*. При расчете стальных конструкций и соединений мостов надлежит учитывать:
коэффициент надежности по назначению gn, принимаемый равным gn = 1,0;
коэффициент надежности gu = 1,3 для элементов конструкций, рассчитываемых по прочности с использованием расчетных сопротивлений Ru;
коэффициент условий работы m, принимаемый по табл. 60* и 81 и подразделам настоящих норм, а для канатов в зоне отгибов на отклоняющих устройствах, хомутов, стяжек, сжимов и анкеров - по обязательному приложению 14.
Таблица 60*
|
Область применения |
Коэффициент
условий работы m |
|
1. Элементы и их соединения в пролетных строениях и опорах железнодорожных и пешеходных мостов при расчете на эксплуатационные нагрузки |
0,9
|
|
2. То же, при расчете на нагрузки, возникающие при изготовлении, транспортировке и монтаже |
1,0 |
|
3. Элементы и их соединения в пролетных строениях и опорах автодорожных и городских мостов при расчете на эксплуатационные нагрузки, а также на нагрузки, возникающие при изготовлении, транспортировании и монтаже |
1,0 |
|
4. Канаты гибких несущих элементов в вантовых и висячих мостах |
0,8 |
|
5. Канаты напрягаемых элементов предварительно напряженных конструкций |
0,9 |
|
6. Растянутые и сжатые элементы из одиночных профилей, прикрепленных одной полкой (или стенкой): |
|
|
неравнополочный уголок, прикрепленный меньшей полкой |
0,7 |
|
то же, прикрепленный большей полкой |
0,8 |
|
равнополочный уголок |
0,75 |
|
прокатный или составной швеллер, прикрепленный стенкой, или тавр, прикрепленный полкой |
0,9 |
|
7. Элементы и их сварные соединения а пролетных строениях и опорах северного исполнения Б |
0,85 |
П р и м е ч а н и я: 1. Значения коэффициента условий работы по поз. 1, 2 и 3 в соответствующих случаях применяются совместно с коэффициентами по поз. 4-7. Коэффициент условий работы по поз. 7 в соответствующих случаях применяется совместно с коэффициентами по поз. 4-6.
2. В случаях, не оговоренных в настоящем разделе, в формулах следует принимать m =1,0.
РАСЧЕТЫ
Общие положения
4.20. Расчетную схему конструкции следует принимать в соответствии с ее проектной геометрической схемой, при этом строительный подъем и деформации под нагрузкой, как правило, не учитываются.
Усилия в элементах и перемещения стальных мостовых конструкций определяются из условия их работы с сечениями брутто.
Геометрическую нелинейность, вызванную перемещением элементов конструкций, следует учитывать при расчете систем, в которых ее учет вызывает изменение усилий и перемещений более чем на 5 %.
При выполнении расчетов с учетом геометрической нелинейности следует определять изменения в направлении действия сил, связанные с общими деформациями системы (следящий эффект).
При определении усилий в элементах конструкций соединения сварные и фрикционные на высокопрочных болтах следует рассматривать как неподатливые.
При расчете вантовых и висячих мостов с гибкими несущими элементами из витых канатов с металлическим сердечником - одинарной свивки и закрытых несущих, подвергнутых предварительной вытяжке согласно п. 4.4*, - надлежит учитывать их продольную и поперечную ползучесть в соответствии с указаниями пп. 4.34 и 4.35.
4.21. Жесткие соединения элементов в узлах решетчатых ферм допускается принимать при расчете шарнирными, если при таком допущении конструкция сохраняет свою неизменяемость, при этом для главных ферм отношение высоты сечения к длине элементов не должно, как правило, превышать 1:15.
Дополнительные напряжения в поясах ферм от деформации подвесок следует учитывать независимо от отношения высоты сечения к длине элемента пояса.
Учет жесткости узлов в решетчатых фермах допускается осуществлять приближенными методами, при этом допускается определение осевых усилий выполнять по шарнирной расчетной схеме.
4.22*. За ось элемента пролетных строений принимается линия, соединяющая центры тяжести его сечений. При определении положения центра тяжести сечения его ослабление отверстиями болтовых соединений не учитывается, а ослабление перфораций учитывается и принимается постоянным по всей длине элемента. При смещении оси элемента сквозных ферм относительно линии, соединяющей центры узлов, эксцентриситет следует учитывать в расчете, если он превосходит:
для П-образных, коробчатых, двухшвеллерных и двутавровых элементов - 1,5 % высоты сечения;
для тавровых и Н-образных элементов - 0,7 % высоты сечения.
Изгибающие моменты от смещения осей элементов распределяются между всеми сходящимися в узле элементами пропорционально их жесткости и обратно пропорционально длине. При этом каждый изгибающий момент следует принимать равным про изведению эксцентриситета на максимальное значение усилия в данном элементе в основной расчетной схеме.
В элементах связей из уголков с болтовыми соединениями, центрированных по рискам, ближайшим к обушку, допускается возникающий при этом эксцентриситет не учитывать.
4.23. Распределение временной нагрузки в элементах многобалочных пролетных строений со сплошными главными балками, объединенными жесткими поперечными связями, при отношении длины пролета к ширине свыше 4 допускается определять по теории тонкостенных стержней, принимая при этом гипотезу о недеформируемости контура поперечного сечения. В остальных случаях необходимо учитывать деформации контура поперечного сечения,
4.24. При проектировании необходимо обеспечивать пространственную неизменяемость, прочность, общую и местную устойчивость пролетных строений и опор в целом, блоков, отдельных элементов, их частей, деталей и соединений под воздействием нагрузок, возникающих при изготовлении, транспортировании и монтаже, под воздействием эксплуатационных нагрузок - и выносливость.
Для элементов, ослабленных отверстиями под обычные болты, при расчетах на прочность и выносливость следует принимать сечения нетто, на устойчивость и жесткость - сечения брутто.
При расчетах элементов с фрикционными соединениями на высокопрочных болтах на выносливость, устойчивость и жесткость следует принимать сечения брутто, при расчетах по прочности - сечения нетто с учетом того, что половина усилия, приходящегося на данный болт, в рассматриваемом сечении уже передана силами трения.
Геометрические характеристики сечения нетто элементов конструкций следует находить, определяя невыгоднейшее ослабление.
Расчеты по прочности
ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ И
ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ
4.25*. Расчет по прочности элементов, подверженных центральному растяжению или сжатию силой N следует выполнять по формуле
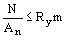 . (141) . (141)
Здесь и в пп. 4.26*-4.32 m - коэффициент условий работы, принимаемый по табл. 60*.
ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ
4.26*. Расчет по прочности элементов, изгибаемых в одной из главных плоскостей, следует выполнять по формуле
М
ѕѕ Ј Ry m , (142)
’Wh
где ’ - коэффициент, учитывающий ограниченное развитие пластических деформаций в сечении и определяемый по формулам (143) и (144)* при условии выполнения требований п. 4.32;
Wn - здесь и далее в расчетах по прочности минимальный момент сопротивления сечения нетто, определяемый с учетом эффективной ширины пояса bef.
При одновременном действии в сечении момента М и поперечной силы Q коэффициент ’ следует определять по формулам:
при tm Ј 0,25 Rs
’ = ’1 ; (143)
при 0,25 Rs < tm Ј Rs
’ = ’1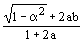 ; (144)* ; (144)*
при этом 0 Ј ’ Ј ’1 ,
где ’1 - коэффициент, принимаемый у двутавровых, коробчатых и тавровых сечений - по табл. 61, для кольцевых сечений - равным 1,15, для прямоугольных сплошных и Н-образных - 1,25;
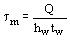 - среднее касательное напряжение в стенке балки, - среднее касательное напряжение в стенке балки,
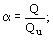 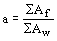 ; ; 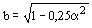 - для коробчатых сечений; - для коробчатых сечений;
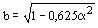 - для двутавровых сечений; - для двутавровых сечений;
здесь Qu - предельная поперечная сила, определяемая по формуле
Rs m ’2 I t
Qu = ѕѕѕѕѕ ,
S
причем ’2 принимается по формуле (160).
Таблица 61
|
Аf,min |
Значения коэффициента ’1 при отношении площадей (Аf,min+Aw)/A, равном |
|
Aw |
0,01 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0 |
1,243 |
1,248 |
1,253 |
1,258 |
1,264 |
1,269 |
1,274 |
1,279 |
1,283 |
1,267 |
1,243 |
|
0,1 |
1,187 |
1,191 |
1,195 |
1,199 |
1,202 |
1,206 |
1,209 |
1,212 |
1,214 |
1,160 |
- |
|
0,2 |
1,152 |
1,155 |
1,158 |
1,162 |
1,165 |
1,168 |
1,170 |
1,172 |
1,150 |
- |
- |
|
0,3 |
1,128 |
1,131 |
1,133 |
1,136 |
1,139 |
1,142 |
1,144 |
1,145 |
1,097 |
- |
- |
|
0,4 |
1,110 |
1,113 |
1,115 |
1,118 |
1,120 |
1,123 |
1,125 |
1,126 |
1,069 |
- |
- |
|
0,5 |
1,097 |
1,099 |
1,102 |
1,104 |
1,106 |
1,109 |
1,110 |
1,106 |
1,061 |
- |
- |
|
0,6 |
1,087 |
1,089 |
1,091 |
1,093 |
1,095 |
1,097 |
1,099 |
1,079 |
- |
- |
- |
|
0,7 |
1,078 |
1,080 |
1,082 |
1,084 |
1,086 |
1,088 |
1,090 |
1,055 |
- |
- |
- |
|
0,8 |
1,071 |
1,073 |
1,075 |
1,077 |
1,079 |
1,081 |
1,082 |
1,044 |
- |
- |
- |
|
0,9 |
1,065 |
1,067 |
1,069 |
1,071 |
1,073 |
1,074 |
1,076 |
1,036 |
- |
- |
- |
|
1,0 |
1,060 |
1,062 |
1,064 |
1,066 |
1,067 |
1,069 |
1,071 |
1,031 |
- |
- |
- |
|
2,0 |
1,035 |
1,036 |
1,037 |
1,038 |
1,039 |
1,040 |
1,019 |
- |
- |
- |
- |
|
3,0 |
1,024 |
1,025 |
1,026 |
1,027 |
1,028 |
1,029 |
1,017 |
- |
- |
- |
- |
|
4,0 |
1,019 |
1,019 |
1,020 |
1,021 |
1,021 |
1,022 |
1,015 |
- |
- |
- |
- |
|
5,0 |
1,015 |
1,015 |
1,016 |
1,017 |
1,018 |
1,018 |
- |
- |
- |
- |
- |
П р и м е ч а н и я: 1. Для коробчатых сечений площадь Аw следует принимать равной сумме площадей стенок.
2. Для таврового сечения площадь Аf,min = 0.
Эффективную ширину пояса bef при вычислении Wn следует определять по формуле
bef = Snbi , (145)
где n - коэффициент приведения неравномерно распределенных напряжений на ширине участков пояса bi к условным равномерно распределенным напряжениям по всей эффективной ширине пояса bef, принимаемый по табл. 62;
bi - ширина участка пояса, заключенная в рассматриваемом сечении между двумя точками с максимальными напряжениями smax (тогда bi = b) или между такой точкой и краем пояса (bi = bk), при этом должны выполняться условия b > 0,04l и bk і 0,02l (в противном случае n = 1);
l - длина пролета разрезной балки или расстояние между точками нулевых моментов в неразрезной балке.
Таблица 62
|
smin / smax |
Коэффициент n |
smin / smax |
Коэффициент n |
|
1,0 |
1 |
0,25 |
0,65 |
|
0,7 |
1 |
0,20 |
0,60 |
|
0,5 |
0,85 |
0,10 |
0,52 |
|
0,33 |
0,72 |
0 |
0,43 |
В табл. 62 обозначено:
smax, smin - максимальное и минимальное напряжения на данном участке пояса шириной bi, определяемые расчетом пространственной конструкции в упругой стадии.
П р и м е ч а н и е. При наличии вырезов в ортотропных плитах для пропуска тела пилона, обрывов плиты в отсеках многосекционного коробчатого сечения, при других нарушениях регулярности конструкции, а также в сечениях, где приложены сосредоточенные силы, значения коэффициента n следует определять по специальной методике.
4.27. Расчет по прочности элементов, изгибаемых в двух главных плоскостях, следует выполнять:
с двутавровыми и коробчатыми сечениями с двумя осями симметрии - по формуле
|Mx| |My|
ѕѕѕ yx + ѕѕѕ yy Ј Ry m ; (146)
’xWxn ’yWyn
с сечениями других типов - по формуле
Mxy Myx
ѕѕѕ yx ± ѕѕѕ yy Ј Ry m ; (147)
’x Ixn ’y Iyn
где ’x, ’y - коэффициенты, определяемые по формулам (143) и (144)* как независимые величины для случаев изгиба относительно осей х и у;
yx, yy - коэффициенты, определяемые:
для двутавровых сечений с двумя осями симметрии - по формулам:
|Mx|
yx = ѕѕѕѕѕ ; yy = 1 ; (148)
’x Wxn Ry m
для коробчатых сечений с двумя осями симметрии - по формулам:
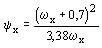 ; ; 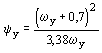 , (149) , (149)
где
|Mx| |My|
wx = ѕѕѕѕѕѕ ; wy = ѕѕѕѕѕѕ . (150)
’x Wxn Ry m ’y Wyn Ry m
ЭЛЕМЕНТЫ, ПОДВЕРЖЕННЫЕ
ДЕЙСТВИЮ ОСЕВОЙ СИЛЫ С ИЗГИБОМ
4.28*. Расчет по прочности внецентренно сжатых, сжато-изгибаемых, внецентренно растянутых и растянуто-изгибаемых элементов при изгибе в одной из главных плоскостей следует выполнять по формуле
N |M|
ѕ y + ѕѕѕ Ј Ry m , (151)
An ’ Wn
где М - приведенный изгибающий момент;
y - коэффициент;
’ - коэффициент, определяемый по формулам (143) и (144)*.
Приведенный изгибающий момент М при гибкости элементов l > 60 для сечений, находящихся в пределах двух средних четвертей длины шарнирно-опертого стержня и всей длины стержня, защемленного по концам, следует определять по формуле
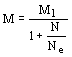 , (152) , (152)
где М1 - момент, действующий в проверяемом сечении;
N - продольная сила, действующая в проверяемом сечении со своим знаком («плюс» - растяжение);
Nе - эйлерова критическая сила в плоскости действия момента, вычисленная для соответствующих закреплений стержня; при l Ј 60 допускается принимать М = М1.
Коэффициент y следует определять:
для элементов двутаврового, коробчатого и таврового сечений с одной осью симметрии по табл. 63 - в случае, если напряжения в меньшем поясе (с площадью Af,min) от момента и продольной силы одинаковых знаков, и по табл. 64* - в случае, если напряжения в меньшем поясе от момента и продольной силы разных знаков;
для элементов сплошного прямоугольного и Н-образного сечений - по формуле
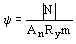 ; (153) ; (153)
для элементов кольцевого сечения - по формуле
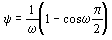 , (154) , (154)
где 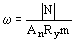 . .
Для других сечений, а также при других закреплениях концов элементов расчет по прочности следует производить по формуле
N My
ѕ + ѕѕѕ Ј Ry m . (155)
An ’ Ixn
В формулах (153) - (155) обозначения те же. что и в формуле (151).
Таблица 63
|
|
Значения коэффициента y при w |
|
|
Af,min |
0,05 |
0,2 |
0,4 |
|
|
Af,max |
при Af,max / Aw |
|
|
|
0,5 |
1 |
2 |
0,5 |
1 |
2 |
0,5 |
1 |
2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
0,5 |
0,53 |
0,55 |
0,57 |
0,63 |
0,68 |
0,78 |
0,77 |
0,85 |
0,92 |
|
|
1 |
0,067 |
0,09 |
0,14 |
0,26 |
0,36 |
0,56 |
0,53 |
0,70 |
0,83 |
|
Окончание табл. 63
|
|
Значения коэффициента y при w |
|
|
Af,min |
0,6 |
0,8 |
0,95 |
|
|
Af,max |
при Af,max / Aw |
|
|
|
0,5 |
1 |
2 |
0,5 |
1 |
2 |
0,5 |
1 |
2 |
|
|
1 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
0,5 |
0,89 |
0,93 |
0,96 |
0,96 |
0,98 |
0,99 |
0,99 |
0,99 |
0,997 |
|
|
1 |
0,78 |
0,87 |
0,93 |
0,92 |
0,95 |
0,97 |
0,98 |
0,99 |
0,994 |
|
В табл. 63 обозначено: 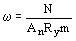 . .
П р и м е ч а н и я: 1. Промежуточные значения коэффициента n определяются линейной интерполяцией.
2. Силу N следует принимать со знаком «плюс». |
Окончание табл. 64*
|
|
Значения коэффициента y при w |
|
|
Af,min |
-0,6 |
-0,8 |
-0,95 |
|
|
Af,max |
при Af,max / Aw |
|
|
|
0,5 |
1 |
2 |
0,5 |
1 |
2 |
0,5 |
1 |
2 |
|
|
1 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
0 |
-0,2 |
-0,2 |
-0,2 |
-0,6 |
-0,6 |
-0,6 |
-0,9 |
-0,9 |
-0,9 |
|
|
0,5 |
-0,49 |
-0,53 |
-0,56 |
-0,76 |
-0,78 |
-0,79 |
-0,94 |
-0,94 |
-0,95 |
|
|
1 |
-0,78 |
-0,87 |
-0,93 |
-0,92 |
-0,95 |
-0,97 |
-0,98 |
-0,99 |
-0,99 |
|
П р и м е ч а н и я: 1. Обозначения см. в табл. 63.
2. Силу N следует принимать со знаком «минус».
3. Промежуточные значения коэффициента y определяются линейной интерполяцией.
4.29*. Расчет по прочности внецентренно сжатых, сжато-изгибаемых, внецентренно растянутых и растянуто-изгибаемых элементов при изгибе в двух главных плоскостях следует выполнять:
для элементов двутаврового, коробчатого и таврового сечений с одной осью симметрии, а также для элементов сплошного прямоугольного и кольцевого сечений - по формуле
1 N |Mx|
ѕ ( ѕ y + ѕѕѕ ) Ј Ry m , (156)
d An ’ Wxn
где |My|
d = 1 - ѕѕѕѕѕѕ ; (157)
’y Wyn Ry m
Mx, My - приведенные изгибающие моменты по п. 4.28*;
y, ’x, ’y - коэффициенты, принимаемые по пп. 4.28* и 4.26*, причем
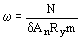 ; ;
для других сечений, а также при других закреплениях концов элементов расчет по прочности следует производить по формуле
N Mx My
ѕ ± ѕѕѕ y ± ѕѕѕ x Ј Ry m . (158)
An ’x Ixn ’y Iyn
В основных случаях, когда приведенных данных для определения ’x и ’y недостаточно, расчет на прочность производят по формуле (158), принимая ’x = ’y = 1.
4.30*. Значения касательных напряжений t в сечениях стенки изгибаемых элементов при М = Мх = Мy = 0 должны удовлетворять условию
QS
t = ѕѕѕ Ј Rs m , (159)
’2 I t
где ’2 = 1,25 - 0,25 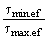 ; (160) ; (160)
tmin.ef, tmax.ef - значения минимального и максимального касательных напряжений в сечении стенки, вычисленные в предположении упругой работы.
При наличии ослабления стенки отверстиями болтовых соединений вместо t в формулу ( 159) следует подставлять значение
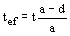 , ,
здесь а - шаг болтов; d - диаметр отверстий.
4.31*. Для стенок балок, рассчитываемых в пп. 4.26* - 4.29*, должно выполняться условие:
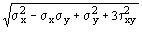 Ј g ў Ry m ; txy Ј Rs m , (161) Ј g ў Ry m ; txy Ј Rs m , (161)
где sx - нормальные (положительные при сжатии) напряжения в проверяемой точке (х, у) срединной плоскости стенки, параллельные оси балки;
sy - такие же напряжения, перпендикулярные оси балки, определяемые согласно обязательному приложению 16*;
gў - коэффициент, равный 1,15 при sx = 0 и 1,10 при sy № 0;
txy - касательное напряжение в проверяемой точке стенки балки.
4.32. Элементы, воспринимающие усилия разных знаков, после проверки прочности с учетом допущения развития ограниченных пластических формаций (’ > 1 ) должны быть проверены также по формуле
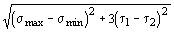 Ј 1,8 Ry m , (162) Ј 1,8 Ry m , (162)
где smax, smin - соответственно расчетные максимальные и минимальные (со своими знаками) нормальные напряжения в проверяемой точке, вычисленные в предположении упругой работы материала;
t1, t2 - касательные напряжения в проверяемой точке (с учетом их знаков), вычисленные соответственно от тех же нагрузок, что и smax и smin.
При невыполнении указанного условия расчет по прочности следует выполнить на наибольшие усилия для упругой стадии работы.
Расчет на прочность и ползучесть стальных канатов
4.33. Расчет по прочности стальных канатов гибких несущих элементов в вантовых и висячих мостах, а также напрягаемых элементов предварительно напряженных конструкций следует выполнять по формуле
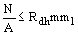 , (163) , (163)
где Rdh - расчетное сопротивление канатов;
m - коэффициент условий работы, принимаемый по табл. 60*:
m1 - коэффициент условий работы, определяемый по обязательному приложению 14.
Расчетное сопротивление Rdh для канатов и пучков из параллельно уложенных высокопрочных проволок определяется по формуле (140), для канатов одинарной свивки и закрытых несущих - по формулам
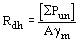 или или 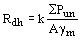 , (164) , (164)
где [SPun] - значение разрывного усилия каната в целом, указанное в государственном стандарте или технических условиях;
gm = 1,6 согласно п. 4.17*;
SPun - сумма разрывных усилий всех проволок в канате;
k - коэффициент агрегатной прочности витого каната, определяемый по табл. 65.
Таблица 65
|
Канат |
Коэффициент k при кратности свивки |
|
|
6 |
8 |
10 |
12 |
14 |
16 |
|
Одинарной свивки |
0,89 |
0,93 |
0,96 |
0,97 |
0,98 |
0,99 |
|
Закрытый несущий |
0,87 |
0,91 |
0,94 |
0,95 |
0,96 |
0,97 |
4.34. Продольную ползучесть epl,x стальных оцинкованных витых канатов с металлическим сердечником - одинарной свивки и закрытых несущих, подвергнутых предварительной вытяжке, - следует определять по формуле
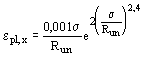 , (165) , (165)
где s - напряжение в канате от усилия, подсчитанного от воздействия нормативных постоянных нагрузок и 1/3 нормативной временной нагрузки;
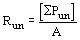 - нормативное сопротивление каната; - нормативное сопротивление каната;
е - основание натуральных логарифмов.
4.35. Поперечную ползучесть epl,y канатов, указанных в п. 4.34, следует определять по формуле
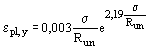 . (166) . (166)
Расчеты по устойчивости
4.36. Расчет при плоской форме потери устойчивости сплошностенчатых элементов замкнутого и открытого сечений, подверженных центральному сжатию, сжатию с изгибом и внецентренному сжатию при изгибе в плоскости наибольшей гибкости, следует выполнять по формуле
 Ј j Ry m , (167) Ј j Ry m , (167)
где j - коэффициент продольного изгиба, определяемый по табл. 1*-3 обязательного приложения 15* в зависимости от гибкости элемента l и приведенного относительного эксцентриситета еef ;
m - здесь и в пп. 4.38-4.41 - коэффициент условий работы, принимаемый по табл. 60*.
Гибкость элемента l следует определять по формуле
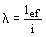 , (168) , (168)
где lef - расчетная длина;
i - радиус инерции сечения относительно оси, перпендикулярной плоскости наибольшей гибкости (плоскости изгиба).
Приведенный относительный эксцентриситет еef следует определять по формуле
eef = h erel , (169)
где h - коэффициент влияния формы сечения, определяемый по обязательному приложению 15*;
erel = 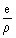 - относительный эксцентриситет плоскости изгиба (здесь е - действительный эксцентриситет силы N при внецентренном сжатии и расчетный эксцентриситет при сжатии с изгибом, r - ядровое расстояние), принимаемый при центральном сжатии равным нулю. - относительный эксцентриситет плоскости изгиба (здесь е - действительный эксцентриситет силы N при внецентренном сжатии и расчетный эксцентриситет при сжатии с изгибом, r - ядровое расстояние), принимаемый при центральном сжатии равным нулю.
Расчетный эксцентриситет е в плоскости изгиба при сжатии с изгибом следует определять по формуле
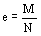 , (170) , (170)
где N, М - расчетные значения продольной силы и изгибающего момента.
Ядровое расстояние r по направлению эксцентриситета следует определять по формуле
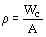 , (171) , (171)
где Wc - момент сопротивления сечения брутто, вычисляемый для наиболее сжатого волокна.
Расчетные значения продольной силы N и изгибающего момента М в элементе следует принимать для одного и того же сочетания нагрузок из расчета системы по недеформированной схеме в предположении упругих деформаций стали.
При этом значения М следует принимать равными:
для элементов постоянного сечения рамных систем - наибольшему моменту в пределах длины элемента;
для элементов с одним защемленным, а другим свободным концом - моменту в заделке, но не менее момента в сечении, отстоящем на треть длины элемента от заделки;
для сжатых поясов ферм, воспринимающих внеузловую нагрузку, - наибольшему моменту в пределах средней трети длины панели пояса, определяемому из расчета пояса как упругой неразрезной балки;
для сжатых стержней с шарнирно-опертыми концами и сечениями, имеющими одну ось симметрии, совпадающую с плоскостью изгиба, - моменту, определяемому по формулам табл. 66.
Таблица 66
|
Относительный эксцентриситет, |
Расчетные значения М при условной гибкости стержня |
|
соответствующий Мmax |
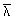 < 4 < 4
|
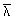 і 4 і 4
|
|
erel Ј 3 |
M=M2=Mmax - 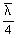 (Mmax -M1) (Mmax -M1) |
M = M1 |
|
3 < erel Ј 20 |
M = M2+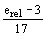 (Mmax -M2) (Mmax -M2) |
M = M1+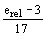 (Mmax -M1) (Mmax -M1) |
В табл. 66 обозначено:
Мmax - наибольший изгибающий момент в пределах длины стержня;
М1 - наибольший изгибающий момент в пределах средней трети длины стержня, но не менее 0,5 Мmax;
еrel - относительный эксцентриситет, определяемый по формуле
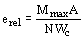 ; ;
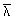 - условная гибкость, определяемая по формуле - условная гибкость, определяемая по формуле
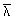 = l aR , = l aR ,
где aR - коэффициент, принимаемый по табл. 4* обязательного приложения 15*.
П р и м е ч а н и е. Во всех случаях следует принимать М і 0,5 Mmax.
Для сжатых стержней с шарнирно-опертыми концами и сечениями, имеющими две оси симметрии, расчетные значения приведенных относительных эксцентриситетов еef следует определять по прил. 6 СНиП II-23-81*, принимая при этом mef равным eef и mef1 равным eef1, определяемому по формуле
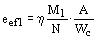 , ,
где M1 - больший из изгибающих моментов, приложенных на шарнирно-опертых концах сжатого стержня указанного типа.
4.37. Расчет при плоской форме потери устойчивости сквозных элементов замкнутого сечения, ветви которых соединены планками или перфорированными листами, при центральном сжатии, сжатии с изгибом и внецентренном сжатии следует выполнять:
элемента в целом в плоскости действия изгибающего момента или предполагаемого (при центральном сжатии) изгиба, перпендикулярной плоскости планок или перфорированных листов, - по формуле (167);
элемента в целом в плоскости действия изгибающего момента или предполагаемого (при центральном сжатии) изгиба, параллельной плоскости планок или перфорированных листов, - по формуле (167) с определением коэффициента продольного изгиба j по табл. 1*-3 обязательного приложения 15* в зависимости от приведенной гибкости lef ;
отдельных ветвей - по формуле (167) в зависимости от гибкости ветви la.
Гибкость ветви la следует определять по формуле (168), принимая за расчетную длину lef расстояние между приваренными планками (в свету) или расстояние между центрами крайних болтов соседних планок, или равное 0,8 длины отверстия в перфорированном листе и за i - радиус инерции сечения ветви относительно собственной оси, перпендикулярной плоскости планок или перфорированных листов.
Приведенную гибкость сквозного элемента lef в плоскости соединительных планок и перфорированных листов следует определять по формуле
lef = 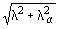 , (172) , (172)
где l - гибкость элемента в плоскости соединительных планок или перфорированных листов, определяемая по формуле (168);
la - гибкость ветви.
При подсчете площади сечения, момента инерции и радиуса инерции элемента следует принимать эквивалентную толщину tef, определяя ее:
для перфорированных листов шириной b, длиной l и толщиной t - по формуле
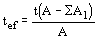 , (173) , (173)
где А = bl - площадь листа до образования перфораций;
SA1 - суммарная площадь всех перфораций на поверхности листа;
для соединительных планок толщиной t - по формуле
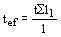 , (174) , (174)
где Sl1 - сумма длин всех планок элемента (вдоль элемента);
l - длина элемента.
Сквозные элементы из деталей, соединенных вплотную или через прокладки, следует рассчитывать как сплошные, если наибольшие расстояния между болтами, приваренными планками (в свету) или между центрами крайних болтов соседних планок не превышают:
для сжатых элементов - 40i;
для растянутых элементов - 80i.
Здесь радиус инерции i уголка или швеллера следует принимать для составных тавровых или двутавровых сечений относительно оси, параллельной плоскости расположения прокладок, для крестовых сечений - минимальный. При этом в пределах длины сжатого элемента должно быть не менее двух прокладок.
4.38. Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых элементов открытого сечения с моментами инерции Ix >Iy, подверженных центральному сжатию силой N, следует выполнять по формуле
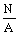 Ј jc Ry m , (175) Ј jc Ry m , (175)
где jc - коэффициент продольного изгиба, определяемый по табл. 1*-3 обязательного приложения 15* при еef = 0 и
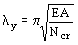 . .
4.39. Расчет на изгибно-крутильную устойчивость сплошностенчатых элементов замкнутого и открытого сечений с моментами инерции Ix > Iy, подверженных сжатию с изгибом и внецентренному сжатию в плоскости наименьшей гибкости, совпадающей с плоскостью симметрии и осью у, следует выполнять по формуле
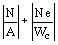 Ј jc Ry m , Ј jc Ry m ,
где e - действительный эксцентриситет силы N при внецентренном сжатии и расчетный эксцентриситет е = M/N при сжатии с изгибом;
Wc - момент сопротивления сечения брутто, вычисляемый для наиболее сжатого волокна:
jc - коэффициент продольного изгиба, определяемый по табл. 1*-3 обязательного приложения 15* при еef = 0 и
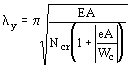 . .
4.40. Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых элементов замкнутого и открытого сечений, подверженных сжатию с изгибом и внецентренному сжатию в двух плоскостях, следует выполнять по формуле
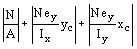 Ј jc Ry m , (177) Ј jc Ry m , (177)
где еy, еx - действительные эксцентриситеты по направлению осей y и х при внецентренном сжатии и расчетные эксцентриситеты при сжатии с изгибом;
ус, хс - координаты наиболее сжатой точки сечения от совместного действия Мх, Мy и N;
jc - коэффициент продольного изгиба, определяемый по табл. 1*-3 обязательного приложения 15* при eef = 0 и
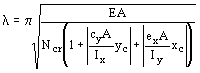 . .
Кроме того, должен быть выполнен расчет по формуле (167) в предположении плоской формы потери устойчивости в плоскости оси y с эксцентриситетом еy (при еx = 0) и в плоскости оси х с эксцентриситетом ex (при ey = 0).
4.41. Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых балок, изгибаемых в одной плоскости, следует выполнять по формуле
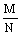 Ј e jb Ry m , (178) Ј e jb Ry m , (178)
где М - наибольший расчетный изгибающий момент в пределах расчетной длины lef сжатого пояса балки;
Wc - момент сопротивления сечения балки для крайнего волокна сжатого пояса;
e - коэффициент, определяемый по формулам:
при ly < 85
e = 1 + (’ - 1) 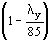 ; ;
при ly і 85
e = 1,0; здесь ’ - коэффициент, определяемый по формулам (143) и (144*);
jb - коэффициент продольного изгиба, определяемый по табл. 1*-3 обязательного приложения 15* при еef = 0 и гибкости из плоскости стенки
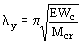 . .
4.42. Расчет при изгибно-крутильной форме потери устойчивости сплошностенчатых балок, изгибаемых в двух плоскостях, следует выполнять по формуле (178), при этом коэффициент jb следует принимать по табл. 1*-3 обязательного приложения 15* при еef = h erel.
Здесь h - коэффициент, принимаемый по обязательному приложению 15*;
еrel - относительный эксцентриситет, определяемый по формуле
erel = 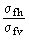 , (179) , (179)
где sfh - наибольшее напряжение в точке на боковой кромке сжатого пояса от изгибающего момента в горизонтальной плоскости в сечении, находящемся в пределах средней трети незакрепленной длины сжатого пояса балки;
sfn - напряжение в сжатом поясе балки от вертикальной нагрузки в том же сечении.
4.43. Проверка общей устойчивости разрезной балки и сжатой зоны пояса неразрезной балки не выполняется в случае, если сжатый пояс объединен с железобетонной или стальной плитой.
Расчет по устойчивости полок и стенок элементов,
не подкрепленных ребрами жесткости
4.44. Расчет по устойчивости полок и стенок прокатных и составных сварных центрально- и внецентренно сжатых, а также сжато-изгибаемых и изгибаемых элементов постоянного поперечного сечения, не подкрепленных ребрами жесткости (черт. 11), следует выполнять по теории призматических складчатых оболочек.
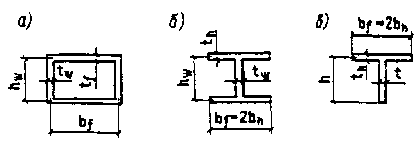
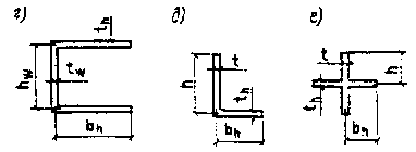
Черт. 11. Схемы расчетных сечений элементов,
не подкрепленных ребрами жесткости
4.45*. Устойчивость полок и стенок элементов, не подкрепленных ребрами жесткости, при среднем касательном напряжении, не превышающем 0,2sх, допускается обеспечивать назначением отношения высоты стенки (h, hw) или ширины полки (br, bh) к толщине (t, tw, tr, th) не более 0,951 a /  (здесь a - коэффициент, sx,cr,ef - приведенное критическое напряжение). (здесь a - коэффициент, sx,cr,ef - приведенное критическое напряжение).
Коэффициент a следует определять:
для пластинок шириной bh, h, опертых по одной стороне (черт. 11, б- е),- по формуле
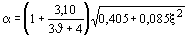 ; (180) ; (180)
для пластинок шириной hw, hv, опертых по двум сторонам (черт. 11, а, б, г), - по формуле
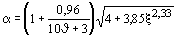 . (181) . (181)
В формулах (180) и (181):
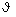 - коэффициент защемления пластинки, определяемый по формулам табл. 67; - коэффициент защемления пластинки, определяемый по формулам табл. 67;
x - коэффициент, определяемый (для сечений брутто) по формуле
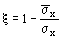 , ,
где sx, 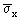 - максимальное и минимальное продольные нормальные напряжения по продольным границам пластинки, положительные при сжатии, определяемые по формулам (141) - (158) при невыгодном для устойчивости пластинки загружении, при этом коэффициенты ’, ’x, ’y, y, yx, yy следует принимать равными 1,0. - максимальное и минимальное продольные нормальные напряжения по продольным границам пластинки, положительные при сжатии, определяемые по формулам (141) - (158) при невыгодном для устойчивости пластинки загружении, при этом коэффициенты ’, ’x, ’y, y, yx, yy следует принимать равными 1,0.
Таблица 67
|
Тип |
Коэффициент защемления пластинки 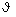 |
|
сечения элемента |
стенки |
полки - для углового сечения
при bh/h |
|
|
|
1 |
0,667 |
0,5 |
|
Коробчатое (черт. 11, а) |
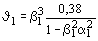
|
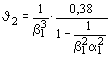
|
|
Двутавровое (черт. 11,б) |
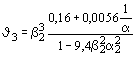
|
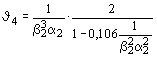
|
|
Тавровое (черт. 11,в) |
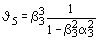
|
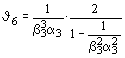
|
|
Швеллерное (черт. 11, г) |
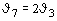
|
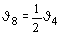
|
|
Угловое для полки высотой h (черт. 11,д) |
- |
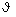 9 = Ґ 9 = Ґ
|
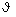 9 = 10 9 = 10
|
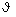 9 = 5,2 9 = 5,2
|
|
Крестовое (черт. 11, е) |
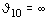
|
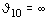
|
В табл. 67 обозначено:
b1 = 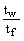 ; a1 = ; a1 = 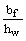 ; b2 = ; b2 = 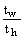 ; a2 = ; a2 = 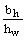 ; b3 = ; b3 = 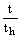 ; a3 = ; a3 = 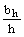 . .
П р и м е ч а н и я: 1. При отрицательном значении знаменателя в формулах табл. 67, а также при равенстве его нулю следует принимать 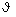 = Ґ. = Ґ.
2. Для углового сечения с отношением bh/h, не указанным в табл. 67, значения 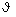 9 следует определять по интерполяции, при этом для bh/h = 1 значение 9 следует определять по интерполяции, при этом для bh/h = 1 значение 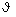 9 следует принимать равным 100. 9 следует принимать равным 100.
Приведенное критическое напряжение sx,cr,ef для пластинки следует определять по формулам табл. 68* в зависимости от критических напряжений sx,cr, за которые следует принимать действующие напряжения sx/m (здесь m - коэффициент условий работы, принимаемый по табл. 60*).
Таблица 68*
|
Марка стали |
Значение sx,cr,
МПа (кг/см2) |
Формулы для определения sx,cr,ef или его значения, МПа (кг/см2) |
|
16Д |
До 176 (1800) |
1,222 sx,cr |
|
Ст3 |
Св. 176 (1800) до 205 (2100) |
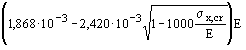
|
|
|
Св. 205 (2100) |
385 (3923) |
|
15ХСНД |
До 186 (1900) |
1,111 sx,cr |
|
|
Св. 186 (1900) до 284 (2900) |
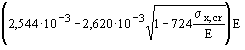
|
|
|
Св. 284 (2900) |
524 (5342) |
|
10ХСНД |
До 206 (2100) |
1,111 sx,cr |
|
390-14Г2АФД |
Св. 206 (2100) до 343 (3499) |
|
|
390-15Г2АФДпс |
Св. 343 (3499) |
591 (6023) |
Расчет по устойчивости полок и стенок элементов,
подкрепленных ребрами жесткости
4.46. Расчет по устойчивости полок и стенок элементов, подкрепленных ребрами жесткости, следует выполнять по теории призматических складчатых оболочек, укрепленных поперечными диафрагмами.
Допускается выполнять расчет по устойчивости пластинок, полок и стенок указанных элементов согласно обязательному приложению 16*.
4.47*. Устойчивость пластинок ортотропных плит допускается обеспечивать назначением отношения их толщины к ширине в соответствии с п. 4.45*, при этом:
для полосовых продольных ребер коэффициент a следует определять по формуле (180) при коэффициенте защемления ns и свесе полки тавра bh (черт. 12, а), равном 0,5 hw при r2 th і hw или r1 th при r2 th < hw;
для участка листа ортотропной плиты между соседними продольными полосовыми ребрами коэффициент a следует определять по формуле (181) при коэффициенте защемления 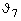 , высоте стенки hw, равной расстоянию между продольными ребрами, и свесе полки bh, равном высоте продольного ребра (черт. 12, б), но не более x1th; здесь x1 и x2 -коэффициенты, определяемые по п. 4.55*. , высоте стенки hw, равной расстоянию между продольными ребрами, и свесе полки bh, равном высоте продольного ребра (черт. 12, б), но не более x1th; здесь x1 и x2 -коэффициенты, определяемые по п. 4.55*.
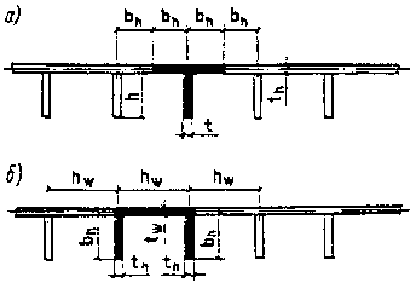
Черт. 12. Схемы расчетных сечений пластинок ортотропных плит
Расчетные длины
4.48. Расчетные длины lef элементов главных ферм, за исключением элементов перекрестной решетки, следует принимать по табл. 69.
Таблица 69
|
|
Расчетная длина lef |
|
Направление продольного изгиба |
поясов |
опорных раскосов
и опорных стоек* |
прочих
элементов
решетки |
|
1. В плоскости фермы |
l |
l |
0,8 l |
|
2. В направлении, перпендикулярном плоскости фермы (из плоскости фермы) |
l1 |
l1 |
l1 |
В табл. 69 обозначено:
l - геометрическая длина элемента (расстояние между центрами узлов) в плоскости фермы:
l1 - расстояние между узлами, закрепленными от смещения из плоскости фермы.
* Расчетную длину опорных раскосов и опорных стоек у промежуточных опор неразрезных пролетных строений следует принимать как для прочих элементов решетки.
4.49. Расчетную длину lef элемента, по длине которого действуют разные сжимающие усилия N1 и N2 (причем N1 > N2), из плоскости фермы (с треугольной решеткой со шпренгелем или полураскосной и т.п.) следует вычислять по формуле
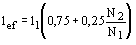 , (182) , (182)
где l1 - расстояние между узлами, закрепленными от смещения из плоскости фермы.
Расчет по устойчивости в этом случае следует выполнять на усилие N1.
Применение формулы (182) допускается при растягивающей силе N2, в этом случае значение N2 следует принимать со знаком «минус», а lef і 0,5 l1.
4.50. Расчетные длины lef элементов перекрестной решетки главной фермы следует принимать:
в плоскости фермы - равными 0,8 l, где l - расстояние от центра узла фермы до точки их пересечения;
из плоскости фермы:
для сжатых элементов - по табл. 70;
для растянутых элементов - равными полной геометрической длине элемента (lef = l1, где l1 см. табл. 69).
Таблица 70
|
Конструкция узла пересечения элементов решетки |
Расчетная длина lef из плоскости фермы
при поддерживающем элементе |
|
|
растянутом |
неработающем |
сжатом |
|
Оба элемента не прерываются |
l |
0,7 l1 |
l1 |
|
Поддерживающий элемент прерывается и перекрывается фасонкой: |
|
|
|
|
рассматриваемый элемент не прерывается |
0,7 l1 |
l1 |
1,4 l1 |
|
рассматриваемый элемент прерывается и перекрывается фасонкой |
0,7 l1 |
- |
- |
4.51. При проверке общей устойчивости балки расчетную длину сжатого пояса следует принимать равной:
расстоянию между узлами фермы продольных связей - при наличии продольных связей в зоне верхних и нижних поясов и поперечных связей в опорных сечениях;
расстоянию между фермами поперечных связей - при наличии продольных связей только в зоне растянутых поясов, при этом фермы поперечных связей должны быть центрированы с узлами продольных связей, а гибкость поясов указанных ферм не должна превышать 100;
пролету балки - при отсутствии в пролете продольных и поперечных связей;
расстоянию от конца консоли до ближайшей плоскости поперечных связей за опорным сечением консоли - при монтаже пролетного строения внавес или продольной надвижкой.
4.52. Расчетную длину lef сжатого пояса главной балки или фермы «открытого» пролетного строения, не имеющего продольных связей по этому поясу, следует определять, как правило, из расчета по устойчивости стержня на упругих опорах, сжатого переменной по длине продольной силой.
Допускается определять указанную расчетную длину по формуле
lef = m l , (183)
где l - длина пояса, равная расчетному пролету для балок и ферм с параллельными поясами, полной длине пояса для балок с криволинейным верхним поясом и ферм с полигональным верхним поясом;
m - коэффициент расчетной длины.
Коэффициент расчетной длины m для поясов балок и ферм с параллельными поясами, а также для фермы с полигональным или балки с криволинейным верхним поясом следует определять по табл. 71, при этом наибольшее перемещение d следует принимать для рамы, расположенной посредине пролета.
Таблица 71
|
x |
Коэффициент m |
|
0 |
0,696 |
|
5 |
0,524 |
|
10 |
0,443 |
|
15 |
0,396 |
|
30 |
0,353 |
|
60 |
0,321 |
|
100 |
0,290 |
|
150 |
0,268 |
|
200 |
0,246 |
|
300 |
0,225 |
|
500 |
0,204 |
|
1000 |
0,174 |
|
Св. 1000 |
0,174 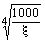 |
В табл. 71 обозначено:
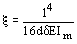 , ,
где d - расстояние между рамами, закрепляющими пояс от поперечных горизонтальных перемещений;
d - наибольшее горизонтальное перемещение узла рамы (исключая опорные рамы) от силы F = 1;
lm - среднее (по длине пролета) значение момента инерции сжатого пояса балки (фермы) относительно вертикальной оси.
П р и м е ч а н и я: 1. Если полученная по данным табл. 71 расчетная длина lef < 1,3d, то ее следует определять из расчета по устойчивости стержня на упругих опорах.
2. Для промежуточных значений x коэффициент m следует определять по линейной интерполяции
Предыдущая часть |
К оглавлению
| Следующая часть
|


![]() , (182)
, (182)![]() ,
,


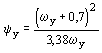 , (149)
, (149)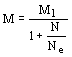 , (152)
, (152)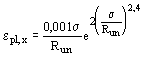 , (165)
, (165)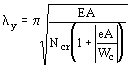 .
.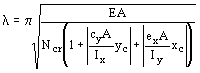 .
.